12 Krzywe Béziera

Ten rozdział będzie zawierał trochę trudniejszy materiał, mam jednak nadzieję, że zapoznasz się z nim w całości. Uważam jednak, iż omówienie rysowania krzywych w reprezentacji Béziera pozwoli na dokładniejsze zrozumienie w jaki sposób są rysowane obiekty w programie, a i pełne pojęcie kolejnych rozdziałów. Aby się nie powtarzać proszę jedynie o dokładne zapoznanie się z rozdziałem "Rysunek rastrowy a wektorowy".

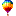Opis krzywych Béziera

Pierre Bézier to francuski matematyk, pracownik firmy Renault. W ramach prac projektowych nad nowymi karoseriami samochodowymi opracował model opisu krzywych.
A teraz odrobina matematyki. Krzywe Béziera są parametrycznymi krzywymi trzeciego stopnia i znajdują szerokie zastosowanie w modelowaniu kształtu figur i powierzchni. Przykładem może tu być modelowanie kształtu nadwozi samochodów. Są one podstawą działania wszystkich poważniejszych programów do tworzenia i edycji rysunków wektorowych (Corel DRAW, Adobe Ilustrator).

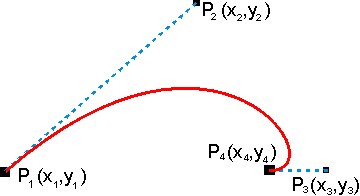
Kształt krzywej Béziera jest określony czterema punktami: dwoma punktami krańcowymi krzywej (tzw. węzłami) (P1, P4) oraz dwoma punktami kontrolnymi (P2, P3). Krzywa interpoluje dwa krańcowe punkty krzywej i aproksymuje dwa punkty kontrolne.

Jeżeli oznaczymy współrzędne tych czterech punktów jako:

P₁ (x₁ , y₁), P₂ (x₂ ,y₂), P₃ (x₃ ,y₃), P₄ (x₄ ,y₄)

to kształt krzywej Béziera określają dwa równania parametryczne:

x_(t) = (1- t)₃ x₁ + 3t (1- t)₂ x₂ + 3t₂ (1- t) x₃ + t₃ x₄

y_(t) = (1- t)₃ y₁ + 3t (1- t)₂ y₂ + 3t₂ (1- t) y₃ + t₃ y₄

gdzie parametr t przybiera wartości z przedziału 0 ≥ t ≥ 1

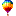Węzły i punkty kontrolne

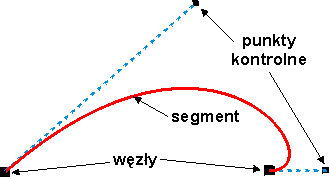
W programie CorelDRAW każdą krzywą (krzywą jest także okrąg, kwadrat, itp.) definiuje się jak już opisałem, podając węzły i punkty kontrolne. Istnieje także pojęcie segmentu w skład którego wchodzą dwa węzły (na jego końcach) i dwa punkty kontrolne. Ponieważ segmenty sąsiadują ze sobą, dlatego z każdym węzłem związane są tylko dwa punkty kontrolne.

Na krzywej możemy wykonać następujące czynności:

1. przesunąć węzeł - zmianie ulegnie wygląd jednego lub dwóch segmentów (gdy węzeł należał do dwóch segmentów),
2. przesunąć punkt kontrolny - zmieni się kształt jednego segmentu,
3. dodać węzeł - jeden segment zostanie podzielony na dwa segmentu, pomiędzy którymi znajdzie się dodany węzeł,
4. usunąć węzeł - zostaną usunięte także dwa punkty kontrolne, a dwa sąsiednie segmenty zostaną połączone w jeden segment, którego kształt będą określały pozostałe-sąsiednie punkty kontrolne,
5. połączyć dwa końcowe węzły - powstanie jeden węzeł z punktami kontrolnymi tak ustawionymi, aby przejście krzywej przez ten węzeł było "gładkie",
6. przekształcić segment na prostą, krzywą, itp. - powoduje to automatyczne ustawienie punktów kontrolnych w ten sposób, aby uzyskać żądany kształt.

Co to oznacza w praktyce? Otóż:

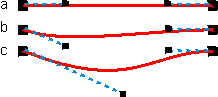
1. jeżeli chcesz uzyskać linię prostą to musisz tak ułożyć punkty kontrolne, aby leżały na linii łączącej oba węzły;
2. gdy przesuniesz jeden z punktów kontrolnych tak, aby nie leżał na prostej łączącej dwa węzły, to wtedy segment "wybrzuszy" się w taki sposób, by w węźle segment był styczny do linii łączącej węzeł z punktem kontrolnym;
3. gdy oddalisz punkt kontrolny od węzła, to krzywa będzie "łagodniej" przechodzić przez węzeł.

  (59 kB)

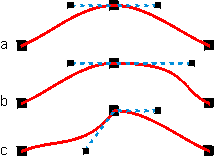
Możemy też wyróżnić trzy charakterystyczne sposoby łączenia segmentów krzywej:

1. punkty kontrolne należące do węzła są symetryczne - otrzymujemy wtedy gładkie przejście krzywej przez węzeł;
2. punkty kontrolne należące do węzła są współliniowe i niesymetryczne - krzywa dalej przechodzi gładko przez węzeł, ale po obu stronach węzła otrzymujemy inny przebieg "wybrzuszeń" krzywej;
3. punkty kontrolne nie są współliniowe - przejście krzywej przez węzeł nie jest gładkie, ponieważ sąsiednie segmenty będą styczne do różnych prostych.

  (23 kB)